Last week, Edward Snowden spoke to a packed crowd at SXSW about the many problems (and limited solutions) facing those of us who want to keep our communications private. Snowden said a number of things — including a shout out to Moxie’s company Whisper Systems, who certainly deserve it. But instead of talking about that, I wanted to focus on (in my opinion) one of Snowden’s most important quotes:
We need all those brilliant Belgian cryptographers to go “alright we know that these encryption algorithms we are using today work, typically it is the random number generators that are attacked as opposed to the encryption algorithms themselves. How can we make them [secure], how can we test them?”
Now it’s possible I’m a little biased, but it seems to me this cuts to the core of our problems with building secure systems in an increasingly hostile world. Namely: most encryption relies on some source of “random” numbers, either to generate keys or (particularly in the case of public key encryption) to provide semantic security for our ciphertexts.
What this means is that an attacker who can predict the output of your RNG — perhaps by taking advantage of a bug, or even compromising it at a design level — can often completely decrypt your communications. The Debian project learned this firsthand, as have many others. This certainly hasn’t escaped NSA’s notice, if the allegations regarding its Dual EC random number generator are true.
All of this brings us back to Snowden’s quote above, and the question he throws open for us. How do you know that an RNG is working? What kind of tests can we run on our code to avoid flaws ranging from the idiotic to the highly malicious? Unfortunately this question does not have an easy answer. In the rest of this post I’m going to try to explain why.
Background: Random and Pseudorandom Number Generation
I’ve written quite a bit about random number generation on this blog, but before we go forward it’s worth summarizing a few basic facts about random number generation.
First off, the ‘random’ numbers we use in most deployed cryptographic systems actually come from two different systems:
- A ‘true’ random number generator (or entropy generator) that collects entropy from the physical world. This can include entropy collected from low-level physical effects like thermal noise and shot noise, or it can include goofy stuff like mouse movements and hard disk seek times.
- An algorithmic ‘pseudorandom number generator’ (PRNG) that typically processes the output of (1) to both stretch the output to provide more bits and, in some cases, provide additional security protections in case the output of (1) proves to be biased.
 |
|
|
If you look at the literature on random number generators, you’ll find a lot of references to statistical randomness testing suites like Diehard or NIST’s SP 800-22. The gist of these systems is that they look a the output of an RNG and run tests to determine whether the output is, from a statistical perspective, “good enough” for government work (very literally, in the case of the NIST suite.)The nature of these tests varies. Some look at simple factors like bias (the number of 1s and 0s) while others look for more sophisticated features such as the distribution of numbers when mapped into 3-D space.Now I don’t want to knock these tests. They’re a perfectly valid way to detect serious flaws in a (true) RNG — I can attest to this, since I’ve built one that failed the tests miserably — but they probably won’t detect flaws in your system. That’s because like I said above, most deployed systems include a combination of RNG and PRNG, or even RNG plus “conditioning” via cryptographic hash functions or ciphers. The nature of these cryptographic, algorithmic processes is such that virtually every processed output will pass statistical tests with flying colors — even if the PRNG is initialized with ‘garbage’ input.This means, unfortunately, that it can be very hard to use statistical tests to detect a broken RNG unless you properly test it only at the low level. And even there you won’t rule outintentional backdoors — as I’ll discuss in a moment.
Runtime Health Checks
Another approach to testing RNGs is to test them while the system is running. This isn’t intended to rule out design-level flaws (as the above statistical and KAT tests are) but it is intended to catch situations where the RNG becomes broken during normal operation. This can occur for a variety of reasons, e.g., manufacturing defects, system damage, and even exposure to outside radiation.
Health checks can take different forms. FIPS 140, for example, mandates that all approved RNGs be tested at startup time using KATs. (This is why you can’t make your test harness conditional on compilation flags — it must ship in your production code!) They subsequently mandate a runtime health check that verifies the generator has not become ‘stuck’, i.e., is spitting out the same bytes over and over again.
While I’m sure this last test may have saved someone, somewhere, it seems totally inappropriate and useless when applied to the output of an RNG/PRNG pair, which is how NIST recommends it be used. This is because even the most broken algorithmic PRNGs will almost never spit out duplicate values — even if the underlying RNG fails completely.
The upshot of this decision is that NIST (FIPS) recommend a check that will almost never succeed in catching anything useful from a PRNG, but does introduce a whole bunch of extra logic that can suffer from flaws and/or malicious circumvention. I’m sure the good folks at NIST realize this, but they recommend it anyway — after all, what else are they going to do?
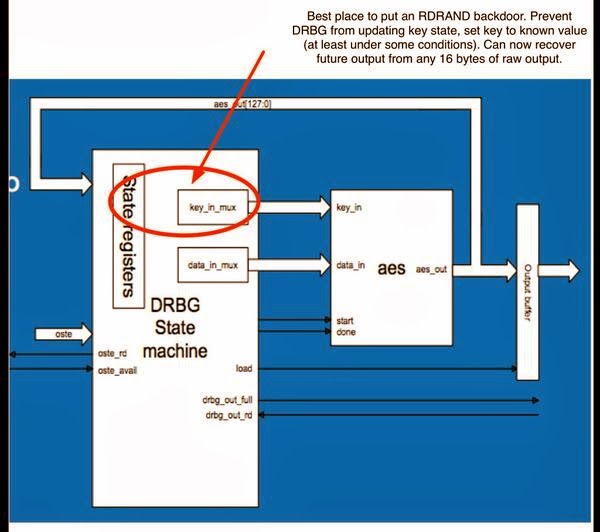 |
| Portion of the Intel Ivy Bridge design, with a few annotations added by yours truly. (original source) |
The CTR-DRBG design relies on two features. First, an AES key is selected at random along with some input seed. This pair goes into the AES cipher, where it is processed to derive a new key and data. The result should be unpredictable to most attackers.
But if you were able to change the way keys were updated (in the key_in_mux hilighted) so that instead of updating the key and/or using an unpredictable one, it chose a fixed key known to the attacker, you would now have a very powerful backdoor. Specifically, the output would still look statistically perfectly random. But an attacker who knows this key could simply decrypt one block of RNG output to obtain all future and past outputs of the generator until the next time it was reseeded.
Note that I am not saying the Intel system has a backdoor in it — far from it. I’m only considering how easily it might be made to have one if you were an attacker with control of Intel’s fabrication plants (or their microcode updates). And this is hardly Intel’s fault. It’s just the nature of this particular RNG design. Others could be just as vulnerable.
Actually using this knowledge to attack applications would be more complex, since many system-level RNGs (including the Linux Kernel RNG) combine the output of the RNG with other system entropy (through XOR, unfortunately, not hashing). But Intel has pushed hard to see their RNG output used directly, and there exist plugins for OpenSSL that allow you to use it similarly. If you used such a method, these hypothetical flaws could easily make their way all the way into your cryptography.
Designing against these issues
Unfortunately, so far all I’ve done is call out the challenges with building trustworthy RNGs. And there’s a reason for this: the challenges are easy to identify, while the solutions themselves are hard. And unfortunately at this time, they’re quite manual.
Building secure RNG/PRNGs still requires a combination of design expertise, careful low-level (true) RNG testing — using expert design and statistical tests — and the use of certified algorithms with proper tests. All of the techniques above contribute to building a secure RNG, but none of them are quite sufficient.
Solving this problem, at least in software, so we can ensure that code is correct and does not contain hidden ‘easter eggs’, represents one of the more significant research challenges facing those of us who depend on secure cryptographic primitives. I do hope some enterprising graduate students will give these issues the attention they deserve.
Notes:
* Though there are some exceptions. See, for example, this FIPS certified smart card that included a bad RNG which was used to generate cryptographic secrets. In general FIPS disallows this except for a very small number of approved RNGs. Perhaps this was one.
Source: Cryptography Engineering
Leave a Reply